Authors¶
Deborah Khider and Alexander James
Preamble¶
Understanding scaling behavior in the climate system is important for several key reasons:
Bridging scales in observations in modeling: the climate system is inherently multiscales, with local feedbacks (e.g., sea ice) influencing global circulation and vice-versa. Scaling analysis can help connecting small-scale processes to large-scale phenomena.
Characterizing natural variability: Many climate variables (temperature precipitation) exhibit power-law scaling in their spectra, meaning variability depends on the timescale of observations. Recognizing these scaling laws can help researchers separate internal from external variability, identify regime shifts or nonlinear feedbacks, and understand persistence and memory in the climate system.
Improving model evaluation and downscaling: Scaling properties provide diagnostics for evaluating how well models reproduce observed variability. If a model fails to capture observed scaling exponents, it may misrepresent key feedbacks or autocorrelation structures. In downscaling, scaling relationships help ensure that fine-scale reconstructions preserve realistic temporal and spatial variability.
In this notebook, we demonstrate the use of the Pyleoclim software package to estimate the spectra from Holocene temperature records and estimate their scaling behavior.
More information about PaleoPAL can be found here.
Technical skills involved:
Loading data in the LiPD format using the
PyLiPDsoftware.Applying and interpreting spectral analysis in with
PyleoclimEstimating scaling exponents from spectra.
Data¶
The data is from the Temperature 12k Database by Kaufman et al. (2020), stored in the Linked PaleoData (LiPD) format on the LiPDVerse.
Reading time¶
15 min
Keywords¶
Pyleoclim; PyLiPD; Holocene; Scaling Behavior; Spectral Analysis.
Let’s import the necessary packages:
# import the necessary packages
# Deal with downloading the LiPD files
import os
import requests
import zipfile
from pathlib import Path
#To mamipulate LiPD Files
from pylipd.lipd import LiPD
# Analysis
import pyleoclim as pyleo
import numpy as np
import pandas as pd
# Visualization
import matplotlib.pyplot as plt
import seaborn as sns
from matplotlib.colors import ListedColormap, BoundaryNorm
from matplotlib.cm import ScalarMappable
# To save
import pickleImporting the Temp12k Database¶
The version of the database used in this notebook can be dowloaded here. The following cell downloads the files and save them locally to a folder called Temp12k:
# Link to LiPD files
temp12_url = 'https://lipdverse.org/Temp12k/current_version/Temp12k1_1_0.zip'
# Download and extract
folder_path = Path("../data/Temp12k")
zip_path = folder_path.with_suffix('.zip')
# Step 1: Check if folder exists, create if not:
folder_path.mkdir(parents=True, exist_ok=True)
# Step 2: Check if folder is empy
if not any(folder_path.iterdir()):
print("Folder is empty. Downloading data...")
# Step 3: Download zip file
response = requests.get(temp12_url)
with open(zip_path, 'wb') as f:
f.write(response.content)
print(f"Downloaded ZIP to {zip_path}")
# Step 4: Extract zip contents into folder
with zipfile.ZipFile(zip_path, 'r') as zip_ref:
zip_ref.extractall(folder_path)
print(f"Extracted contents to {folder_path}")
The next step is to create a pylipd.LiPD object from these files.
agent code Use PyLiPD to create a LiPD object from the files in the directory: “../data/Temp12k”
# This code snippet creates a LiPD object and loads data from the specified directory "../data/Temp12k". It then prints the names of all the datasets loaded into the LiPD object to verify that the data has been successfully imported.
# Auto-generated by PaleoPal CodeGenerationAgent with contextual search
# Import LiPD
#from pylipd.lipd import LiPD
# Create a LiPD object and load the data from the directory
lipd = LiPD()
lipd.load_from_dir("../data/Temp12k")
# Verify loaded datasets by printing their names
#print(lipd.get_all_dataset_names())Loading 697 LiPD files
100%|██████████| 697/697 [00:16<00:00, 41.49it/s]Loaded..
Next, let’s get some of the essential information to work with these timeseries. LiPD objects have a method called get_timeseries_essentials that can be useful in that regard.
agent code
Use the method get_timeseries_essentials to load the information.
# This code snippet loads timeseries essentials from the Temp12k database using a LiPD object. It first ensures the data is loaded from the specified directory and then retrieves the timeseries essentials using the get_timeseries_essentials method, storing the result in a DataFrame for examination.
# Auto-generated by PaleoPal CodeGenerationAgent with contextual search
#from pylipd.lipd import LiPD
# Create a LiPD object if not already created
#lipd = LiPD()
# Load data from the directory if not already loaded
#lipd.load_from_dir('../data/Temp12k')
# Get the timeseries essentials
# This will return a pandas DataFrame or similar structure with timeseries information
#try:
df = lipd.get_timeseries_essentials()
# Print the DataFrame to review the essential information
#print(df_timeseries_essentials)
#except Exception as e:
#print(f'An error occurred while getting timeseries essentials: {e}')display(df.head())Let’s filter for temperature only:
df_filt = df[df['paleoData_variableName']=='temperature']
print(f"We have {len(df_filt)} timeseries")We have 2201 timeseries
display(df_filt.head())Load the resulting timeseries into Pyleoclim¶
Now that we have extracted the essential information from the LiPD files, let’s put our timeseries into a MultipleGeoSeries object so we can work with them more easily:
agent code Using each row in df_filt, create a Pyleoclim MultipleGeoseries object
# This code creates a Pyleoclim MultipleGeoSeries object from each row in a filtered DataFrame (df_filt) using essential timeseries information. It iterates through the DataFrame rows, constructing a GeoSeries object for each row, which is then appended to a list. Finally, a MultipleGeoSeries object is created from this list, allowing for further paleoclimate analysis.
# Auto-generated by PaleoPal CodeGenerationAgent with contextual search
# Import necessary library
#import pyleoclim as pyleo
# Create a list to hold GeoSeries objects
ts_list = []
# Iterate over each row in the DataFrame containing filtered timeseries\# Create a GeoSeries object for each row
for _, row in df_filt.iterrows():
if row['time_values'] is not None and row['paleoData_values'] is not None: #there seems to be missing entries in the database (added by DK)
if np.all(np.isnan(row['time_values'])) == False and np.all(np.isnan(row['paleoData_values'])) == False: #check that not all the values are false (added by DK)
ts = pyleo.GeoSeries(
time=row['time_values'],
value=row['paleoData_values'],
time_name=row['time_variableName'],
value_name=row['paleoData_variableName'],
time_unit=row['time_units'],
value_unit=row['paleoData_units'],
lat=row['geo_meanLat'],
lon=row['geo_meanLon'],
elevation=row.get('geo_meanElev'), # Use get to handle missing values
observationType=row['paleoData_proxy'],
archiveType=row['archiveType'],
verbose=False,
label=row['dataSetName'] + '_' + row['paleoData_variableName']
)
ts_list.append(ts)
else:
pass
else:
pass
# Create a MultipleGeoSeries object from the list of GeoSeries objects
geoms = pyleo.MultipleGeoSeries(ts_list, label='Temp12k', time_unit='years BP')
# Display or process the MultipleGeoSeries object
# print(multiple_geoseries) # Uncomment to see details of the objectprint(f"We have {len(geoms.series_list)} timeseries left")We have 2182 timeseries left
Let’s map the location of these records!
agent code Map the records contained in geoms.
# This code snippet uses the MultipleGeoSeries object 'geoms' to create a map of the records using the 'map' method in Pyleoclim. The records are displayed in a Robinson projection with a specified figure size and color-coded by 'archiveType'.
# Auto-generated by PaleoPal CodeGenerationAgent with contextual search
# This code maps the records contained in the 'geoms' which is a MultipleGeoSeries object.
# Ensure that the pylipd and pyleoclim packages are installed and available for import.
# Import necessary package for plotting geographically distributed data
#import pyleoclim as pyleo
# 'geoms' is assumed to be a MultipleGeoSeries object already created from the DataFrame 'df_filt'
# Map the records
fig, ax = geoms.map(projection='Robinson', figsize=[12, 6], hue='archiveType')
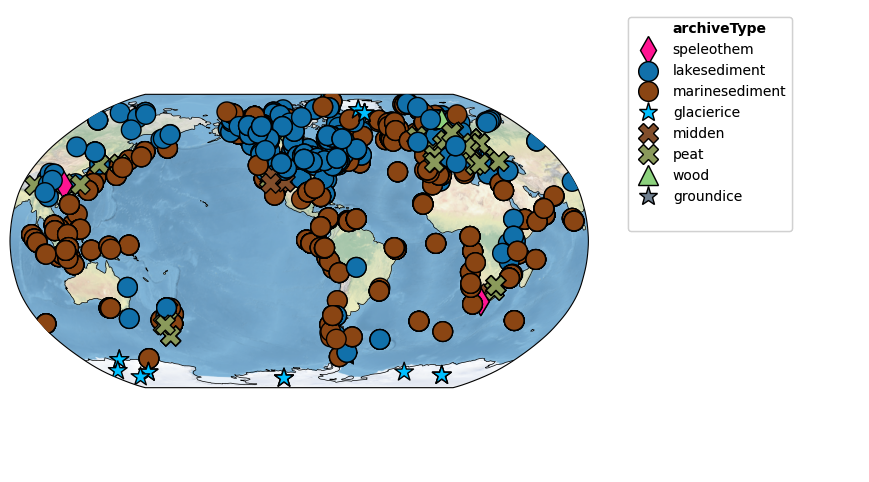
Estimating scaling behavior using Pyleoclim¶
Applying the WWZ method¶
Now we are ready to perform spectral analysis on our MultipleGeoSeries object! For this application, we need to use the Weighted Wavelet Z-Transform (Kirchner and Neal, 2013) for power spectral density (PSD) calculation since the Lomb-Scargle periodogram has a known bias when estimating the slope.
For analysis, each timeseries will be standardized prior to PSD estimation.
agent code Perform spectral analysis on geoms using the WWZ method and using a log frequency vector. Standardize before spectral analysis.
# This code performs spectral analysis on a standardized MultipleGeoSeries object using the Weighted Wavelet Z-Transform (WWZ) method with a log frequency vector. The standardized data, 'geoms_standardized', is analyzed and the resulting Power Spectral Density (PSD) is plotted.
# Auto-generated by PaleoPal CodeGenerationAgent with contextual search
# Import necessary packages
#import pyleoclim as pyleo
#import matplotlib.pyplot as plt
# Standardize the 'geoms' MultipleGeoSeries object before spectral analysis
#geoms_standardized = geoms.standardize(keep_log=False) #keep log is not in MultipleSeries
geoms_standardized = geoms.standardize()
# Perform spectral analysis using the WWZ method with a log frequency vector
psd_wwz = geoms_standardized.spectral(method='wwz', freq='log')
# Plot the resultant Power Spectral Density (PSD) (might be too many to plot)
#fig, ax = psd_wwz.plot(title='PSD using WWZ method with log frequency vector')
#plt.show()Performing spectral analysis on individual series: 0%| | 0/2182 [00:00<?, ?it/s]OMP: Info #276: omp_set_nested routine deprecated, please use omp_set_max_active_levels instead.
OMP: Info #276: omp_set_nested routine deprecated, please use omp_set_max_active_levels instead.
OMP: Info #276: omp_set_nested routine deprecated, please use omp_set_max_active_levels instead.
OMP: Info #276: omp_set_nested routine deprecated, please use omp_set_max_active_levels instead.
OMP: Info #276: omp_set_nested routine deprecated, please use omp_set_max_active_levels instead.
OMP: Info #276: omp_set_nested routine deprecated, please use omp_set_max_active_levels instead.
OMP: Info #276: omp_set_nested routine deprecated, please use omp_set_max_active_levels instead.
OMP: Info #276: omp_set_nested routine deprecated, please use omp_set_max_active_levels instead.
OMP: Info #276: omp_set_nested routine deprecated, please use omp_set_max_active_levels instead.
OMP: Info #276: omp_set_nested routine deprecated, please use omp_set_max_active_levels instead.
OMP: Info #276: omp_set_nested routine deprecated, please use omp_set_max_active_levels instead.
OMP: Info #276: omp_set_nested routine deprecated, please use omp_set_max_active_levels instead.
Performing spectral analysis on individual series: 100%|██████████| 2182/2182 [24:59<00:00, 1.46it/s]
Since this calculation takes a while to perform, let’s pickle the results for future use:
#with open("../data/temp12k_scaling.pkl", "wb") as f: # 'wb' = write binary
#pickle.dump(psd_wwz, f)Let’s look at the various spectra, color-coding them by latitude:
#If needed, re-open the pickle file.
with open("../data/temp12k_scaling.pkl", "rb") as f: # 'rb' = read binary
psd_wwz = pickle.load(f)The easiest way to proceed is to create a DataFrame with the necessary information:
label = []
lat = []
lon = []
archive = []
amp =[]
period = []
unit = []
#grab the information
for item in psd_wwz.psd_list:
label.append(item.timeseries.label)
lat.append(item.timeseries.lat)
lon.append(item.timeseries.lon)
archive.append(item.timeseries.archiveType)
amp.append(item.amplitude)
period.append(1/item.frequency)
unit.append(item.period_unit)
# Put it in a DataFrame
df_psd = pd.DataFrame({'Name':label,
'Latitude':lat,
'Longitude':lon,
'Archive':archive,
'Amplitude':amp,
'Period':period,
'Units':unit})
display(df_psd.head())Make the figure:
# --- 0) Seaborn style
sns.set_theme(style="whitegrid", context="talk") # 'talk' or 'poster' increases fonts
plt.rcParams.update({
"font.size": 14,
"axes.labelsize": 16,
"axes.titlesize": 18,
"xtick.labelsize": 12,
"ytick.labelsize": 12,
"legend.fontsize": 12,
})
# --- 1) Ensure arrays, explode to long-form (aligned lengths required)
# If arrays are lists/np arrays per row, this works in pandas >= 1.3
df_long = df_psd.copy()
# Coerce to list for safety
df_long["Amplitude"] = df_long["Amplitude"].apply(lambda x: np.asarray(x).tolist())
df_long["Period"] = df_long["Period"].apply(lambda x: np.asarray(x).tolist())
# Add a series id (one per original row) so each becomes one line after explode
df_long["series_id"] = np.arange(len(df_long))
# Explode both columns (lists must have same length per row)
df_long = df_long.explode(["Period", "Amplitude"], ignore_index=True)
# Make numeric + drop NaNs / non-finite
df_long["Period"] = pd.to_numeric(df_long["Period"], errors="coerce")
df_long["Amplitude"] = pd.to_numeric(df_long["Amplitude"], errors="coerce")
df_long = df_long.replace([np.inf, -np.inf], np.nan).dropna(subset=["Period", "Amplitude", "Latitude"])
# --- 2) Build absolute-latitude bins every 10°
abs_lat = np.abs(df_long["Latitude"])
# Bins: [0,10), [10,20), ..., [80,90]; include_lowest=True puts 0° into first bin
bins = np.arange(0, 100, 10) # 0..90 by 10
labels = [f"{b:02d}–{b+10:02d}°" for b in bins[:-1]] # 0–10°, 10–20°, ...
df_long["lat_bin"] = pd.cut(abs_lat, bins=bins, right=False, include_lowest=True, labels=labels)
# Keep only rows that fell into a defined bin
df_long = df_long.dropna(subset=["lat_bin"])
# --- 3) Custom palette per your mapping
# Start from RdBu_r, reverse, then splice BuGn_r(1:4) into positions [3:6]
cmap_base = sns.color_palette("RdBu_r", 9)[::-1] # list of 9 RGB tuples
cmap_green = sns.color_palette("BuGn_r") # default ~10 colors
cmap_base[3:6] = cmap_green[1:4] # replace indices 3,4,5
listed_cmap = ListedColormap(cmap_base)
# Map bins to integer indices 0..8 in order of labels
bin_to_idx = {lab: i for i, lab in enumerate(labels)}
df_long["lat_bin_idx"] = df_long["lat_bin"].map(bin_to_idx)
# --- 4) Plot: one line per series, colored by lat_bin (discrete)
fig, ax = plt.subplots(figsize=(10, 6))
# We'll loop to guarantee exact color mapping & line-by-line control, while still using seaborn aesthetics
for (sid, latbin_idx), g in df_long.groupby(["series_id", "lat_bin_idx"], sort=False):
ax.plot(
g["Period"].values,
g["Amplitude"].values,
lw=1.2,
alpha=0.9,
color=listed_cmap(latbin_idx) if pd.notna(latbin_idx) else "0.6",
)
# Log scale on x/y
ax.set_xscale("log")
ax.set_yscale("log")
ax.invert_xaxis()
# Reduce limits on y axis
ax.set_ylim(1e-6, 1e6)
# Redo the x ticks
period_ticks = [2, 5, 10, 20, 100, 1000, 10000, 100000, 1000000]
period_ticklabels = ['2', '5', '10', '20', '100', '1 k', '10 k', '100 k', '1 m']
ax.set_xticks(period_ticks)
ax.set_xticklabels(period_ticklabels)
# Labels (try to pull a single units label if unique)
y_units = None
if "Units" in df_long and df_long["Units"].nunique(dropna=True) == 1:
y_units = df_long["Units"].dropna().iloc[0]
ax.set_xlabel(f"Period ({y_units})" if y_units else "Period")
ax.set_ylabel("PSD")
# --- 5) Discrete colorbar for the 10° abs-lat bins (top ticks + top label)
bounds = np.arange(-0.5, 9.5, 1) # boundaries: -0.5, 0.5, ..., 8.5
norm = BoundaryNorm(boundaries=bounds, ncolors=listed_cmap.N)
sm = ScalarMappable(norm=norm, cmap=listed_cmap)
sm.set_array([])
# ticks exactly at bin edges → labels 0,10,...,90
tick_positions = np.arange(-0.5, 9.5, 1)
tick_labels = [str(i * 10) for i in range(10)] # 0..90
cbar = fig.colorbar(
sm, ax=ax, boundaries=bounds, ticks=tick_positions, orientation='vertical'
)
cbar.set_ticklabels(tick_labels) # numbers at the edges
cbar.ax.tick_params(labelsize=12)
# label
cbar.ax.set_ylabel("Latitude (°N/°S)", fontsize=16)
# --- 6) Style grid and axes lines
# Make grid dashed
ax.grid(True, which='major', linestyle='--', linewidth=0.8, color='gray', alpha=0.6)
ax.grid(True, which='minor', linestyle='--', linewidth=0.5, color='gray', alpha=0.4)
# Make the axis spines black and a bit thicker
for spine in ax.spines.values():
spine.set_color('black')
spine.set_linewidth(1.2)
# --- 7) Nice touches
plt.tight_layout()
plt.show()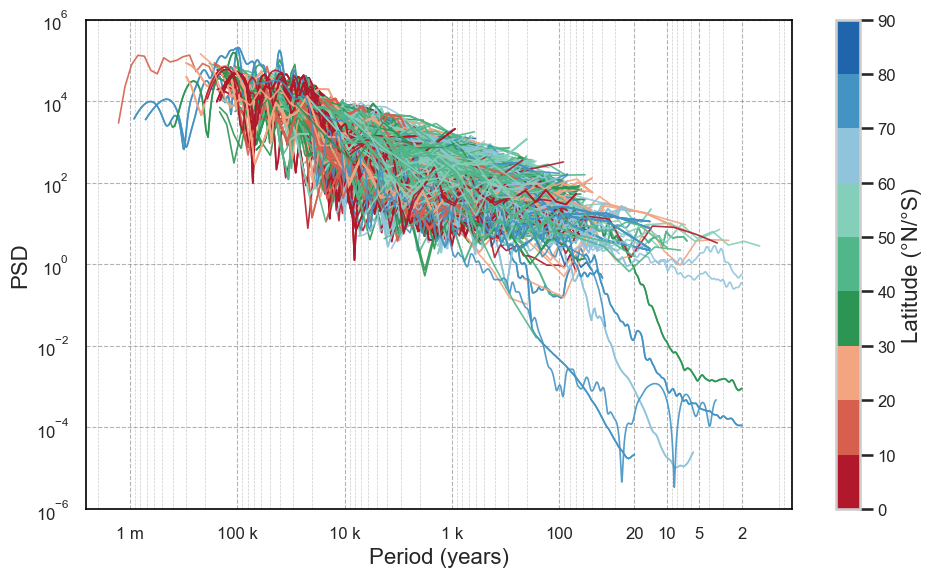
Scaling slope estimation¶
Once the PSD is calculated for each record, we may estimate the scaling slope of the PSD curves using the .beta_est() method.
We can specify two arguments for the .beta_est() method:
fmin: which defines the minimum frequency edge of the range for estimationfmax: which defines the maxmimum frequency edge of the range for estimation
We will calculate three sets of the scaling factors:
beta_S: period over [10, 100] yrsbeta_M: period over [100, 1000] yrsbeta_L: period over [1000, 10000] yrs
agent code For the psd_wwz object, can you calculate the scaling exponent. I want to calculate it with various values for the fmin and fmax parameters (fmin,fmax) as (1/100, 1/10), (1/1000, 1/100) and (1/10000, 1/1000). The resulting scaling exponent should be stored in the following variables: beta_S, beta_M and beta_L.
# This code calculates the scaling exponent (beta) for a Power Spectral Density (PSD) object using the beta estimation method provided by the Pyleoclim library. The calculation is performed over three frequency ranges to yield beta_S, beta_M, and beta_L, which represent scaling exponents over short, medium, and long periods, respectively. The results are stored in the variables beta_S, beta_M, and beta_L, and are printed to the console.
# Auto-generated by PaleoPal CodeGenerationAgent with contextual search
# Calculate the scaling exponent (beta) for the psd_wwz object
# Import necessary libraries
#import pyleoclim as pyleo
# Define frequency bounds for beta calculations
frequency_ranges = [
{'name': 'S', 'fmin': 1/100, 'fmax': 1/10},
{'name': 'M', 'fmin': 1/1000, 'fmax': 1/100},
{'name': 'L', 'fmin': 1/10000, 'fmax': 1/1000}
]
# Initialize dictionary to store beta values
beta_values = {}
# Calculate beta for each frequency range
for freq_range in frequency_ranges:
# Calculate beta using the beta_est method
beta_est_res = psd_wwz.beta_est(fmin=freq_range['fmin'], fmax=freq_range['fmax'])
# Store result in the dictionary using the frequency range name as the key
beta_values[f"beta_{freq_range['name']}"] = beta_est_res
# Retrieve the calculated beta values
beta_S = beta_values['beta_S'].beta_est_res['beta']
beta_M = beta_values['beta_M'].beta_est_res['beta']
beta_L = beta_values['beta_L'].beta_est_res['beta']
# Print the results
print(f"beta_S: {beta_S}")
print(f"beta_M: {beta_M}")
print(f"beta_L: {beta_L}")
# Transform into numpy arrays
beta_S = np.array(beta_S)
beta_M = np.array(beta_M)
beta_L = np.array(beta_L)Let’s see how many of the calculated slopes are not NaNs:
print(f"There are {len(beta_S[~np.isnan(beta_S)])} records for which the slope could be calculated in for periods between 10-100 year periods")
print(f"There are {len(beta_M[~np.isnan(beta_M)])} records for which the slope could be calculated in for periods between 100-1,000 year periods")
print(f"There are {len(beta_L[~np.isnan(beta_L)])} records for which the slope could be calculated in for periods between 1,000-10,000 year periods")There are 19 records for which the slope could be calculated in for periods between 10-100 year periods
There are 225 records for which the slope could be calculated in for periods between 100-1,000 year periods
There are 1019 records for which the slope could be calculated in for periods between 1,000-10,000 year periods
Visualization of scaling behavior¶
Let’s visualize our results in a few different ways:
A simple histogram/Kernel Density Estimation (KDE) of the slopes ( values) for the various periods considered here.
A spatial map with symbols representing the types of archive and the map the value of the slopes.
Kernel Density Estimation¶
# --- Clean data: drop NaNs
beta_S_clean = np.array(beta_S)[~np.isnan(beta_S)]
beta_M_clean = np.array(beta_M)[~np.isnan(beta_M)]
beta_L_clean = np.array(beta_L)[~np.isnan(beta_L)]
# --- Compute medians and sample sizes
med_s = np.median(beta_S_clean)
med_m = np.median(beta_M_clean)
med_l = np.median(beta_L_clean)
n_s = beta_S_clean.shape[0]
n_m = beta_M_clean.shape[0]
n_l = beta_L_clean.shape[0]
# --- Plot
sns.set_theme(style="whitegrid", context="talk")
fig, ax = plt.subplots(figsize=[8, 6])
ax.set_xlim([-5, 10])
ax.set_ylim(0, 0.8)
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
# --- KDEs
g1 = sns.kdeplot(beta_S_clean, fill=False, color=sns.xkcd_rgb['denim blue'], linestyle='-',
label=rf'$\beta_S$ = {med_s:.2f} (10–100 yrs, {n_s} records)', ax=ax)
ax.axvline(x=med_s, ymin=0, ymax=0.1, linewidth=1, color=sns.xkcd_rgb['denim blue'], linestyle='-')
g2 = sns.kdeplot(beta_M_clean, fill=False, color=sns.xkcd_rgb['medium green'], linestyle='-',
label=rf'$\beta_M$ = {med_m:.2f} (100–1000 yrs, {n_m} records)', ax=ax)
ax.axvline(x=med_m, ymin=0, ymax=0.1, linewidth=1, color=sns.xkcd_rgb['medium green'], linestyle='-')
g3 = sns.kdeplot(beta_L_clean, fill=False, color=sns.xkcd_rgb['pale red'], linestyle='-',
label=rf'$\beta_L$ = {med_l:.2f} (1–10 kyr, {n_l} records)', ax=ax)
ax.axvline(x=med_l, ymin=0, ymax=0.1, linewidth=1, color=sns.xkcd_rgb['pale red'], linestyle='-')
# --- Labels & legend
ax.legend(fontsize=13, loc='upper right', bbox_to_anchor=(1, 1))
ax.set_ylabel('KDE', fontsize=14)
ax.set_xlabel(r'$\beta$', fontsize=14)
# --- Grid & spine styling (dashed grid, black axes)
ax.grid(True, which='major', linestyle='--', linewidth=0.8, color='gray', alpha=0.6)
ax.grid(True, which='minor', linestyle='--', linewidth=0.5, color='gray', alpha=0.4)
for spine in ['bottom', 'left']:
ax.spines[spine].set_color('black')
ax.spines[spine].set_linewidth(1.2)
plt.tight_layout()
plt.show()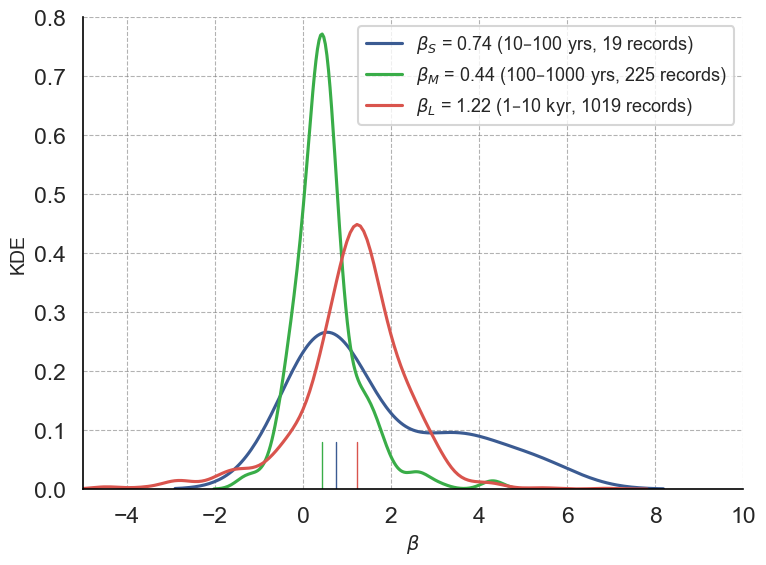
We see that scaling exponents cover a broad range.
Let’s have a look at each scaling exponent range by the type of archive and location
Spatial visualization¶
Let’s first create MultipleGeoSeries objects that contain the records for which there is a scaling estimate at each period interval of interest.
idx_nan_S = np.where(np.isnan(beta_S))[0]
idx_nan_M = np.where(np.isnan(beta_M))[0]
idx_nan_L = np.where(np.isnan(beta_L))[0]
# Collect labels for NaNs in each array
labels_nan_S = [geoms.series_list[i].label for i in idx_nan_S]
labels_nan_M = [geoms.series_list[i].label for i in idx_nan_M]
labels_nan_L = [geoms.series_list[i].label for i in idx_nan_L]And remove these datasets from the original MultipleGeoSeries object geoms:
geoms_S=geoms.copy()
for item in labels_nan_S:
geoms_S.remove(item)
geoms_M=geoms.copy()
for item in labels_nan_M:
geoms_M.remove(item)
geoms_L=geoms.copy()
for item in labels_nan_L:
geoms_L.remove(item)Let’s map them one-by-one.
Scaling exponent - 10-100 year period¶
To make use of Pyleoclim’s mapping capabilities, let’s add the beta attribute to each GeoSeries in the MultipleGeoSeries object geoms_S:
geoms_S_hue = geoms_S.copy()
for i, ser in enumerate(geoms_S_hue.series_list):
ser.beta = beta_S_clean[i]
fig,ax = geoms_S_hue.map(hue = 'beta', cmap = 'viridis', projection='Robinson', proj_default={"central_longitude":0})
ax['cb'].set_ylim([0, 5])
ax['cb'].set_ylabel(r'$\beta$', fontsize=14)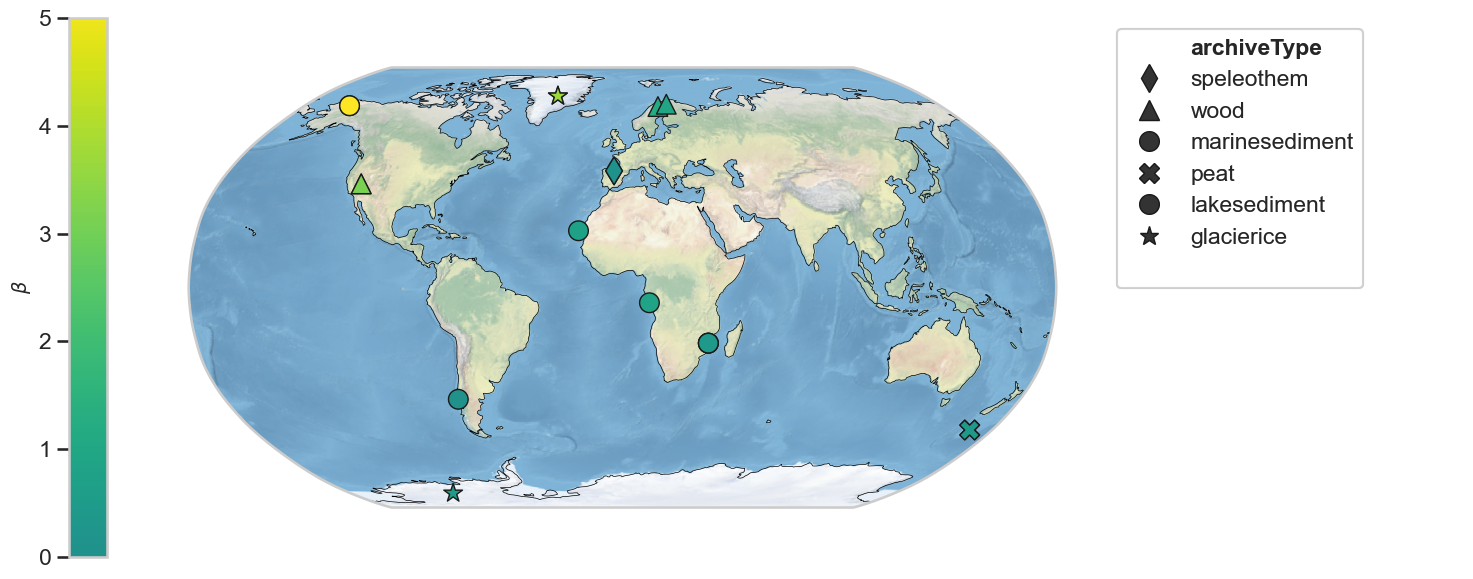
Scaling exponent - 100-1000 year period¶
geoms_M_hue = geoms_M.copy()
for i, ser in enumerate(geoms_M_hue.series_list):
ser.beta = beta_M_clean[i]
fig,ax = geoms_M_hue.map(hue = 'beta', cmap = 'viridis', projection='Robinson', proj_default={"central_longitude":0})
ax['cb'].set_ylim([-1, 4])
ax['cb'].set_ylabel(r'$\beta$', fontsize=14)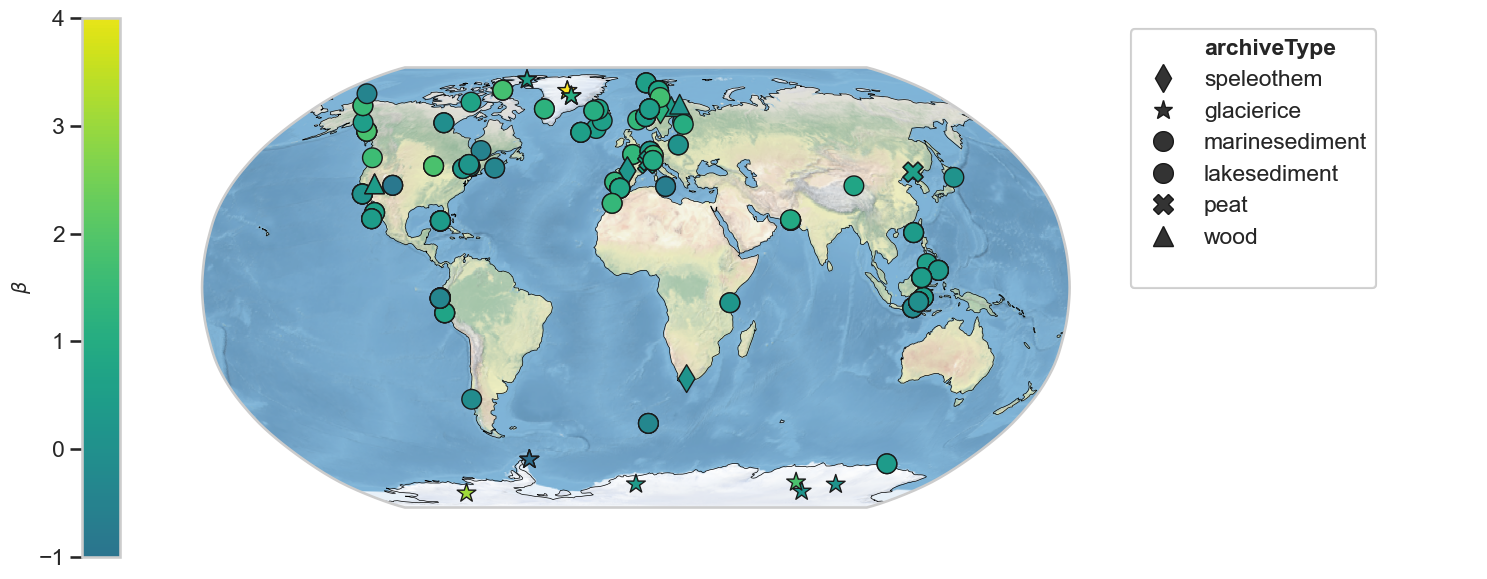
Scaling exponent - 1000-10000 year period¶
geoms_L_hue = geoms_L.copy()
for i, ser in enumerate(geoms_L_hue.series_list):
ser.beta = beta_L_clean[i]
fig,ax = geoms_L_hue.map(hue = 'beta', cmap = 'viridis', projection='Robinson', proj_default={"central_longitude":0})
ax['cb'].set_ylim([-6.5, 6.5])
ax['cb'].set_ylabel(r'$\beta$', fontsize=14)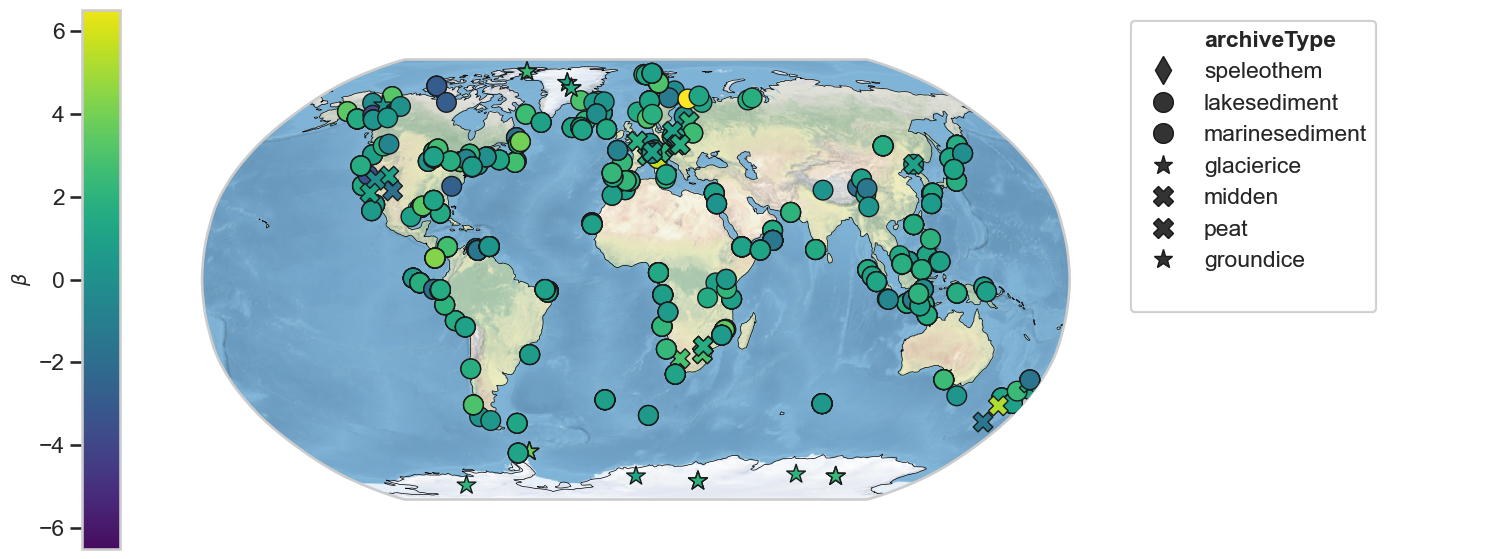
- Kaufman, D., McKay, N., Routson, C., Erb, M., Dätwyler, C., Sommer, P. S., Heiri, O., & Davis, B. (2020). Holocene global mean surface temperature, a multi-method reconstruction approach. Scientific Data, 7(1). 10.1038/s41597-020-0530-7
- Kirchner, J. W., & Neal, C. (2013). Universal fractal scaling in stream chemistry and its implications for solute transport and water quality trend detection. Proceedings of the National Academy of Sciences, 110(30), 12213–12218. 10.1073/pnas.1304328110