Creating Toy Data#
This notebook lays out the details of how we use Pyleoclim to calculate correlation between insolation and toy data, in order to illustrate the difficulty in distinguishing between seasonal and physical lag when conducting this analysis.
The notebook is structured as follows:
Define a function that will be used to calculate correlations between records that contain large hiatuses
Create sinusoidal toy data
Define insolation curves using climlab
Calculate correlation between shifted insolation and toy data
Define further seasonal insolation curves using climlab
Calculate correlation between seasonal insolation and toy data
Plot results
# Importing relevant packages
import math
from tqdm import tqdm
import pyleoclim as pyleo
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
from climlab.solar.orbital import OrbitalTable
from climlab.solar.insolation import daily_insolation
Here we create our correlate_hiatus_series function. This function essentially removes the hiatuses from one series (in this case, series1), aligns the remaining time axis with series2, and calculates the correlation between these records.
Note that this function makes the interpretation of significance very difficult. None of the usual measures of significance apply here, as we’re destroying much of the temporal information in series1 by removing the hiatuses and placing the series on a dummy time axis for correlation purposes. In this case, since we’re using continuous toy data, this isn’t too important, but it will matter later on!
def correlate_hiatus_series(series1, series2, cutoff_scale1=None):
"""Function to correlate series with large gaps. This is done by segmenting the time series, smoothing (if this is desired),
and then reconnecting the time series with a dummy time axis so as not to re-introduce the hiatuses.
series1 : pyleoclim.Series
One series to correlate, presumed to have hiatuses
series2 : pyleoclim.Series
Other series to correlate, presumed to not have hiatuses
cutoff_scale : int
Cutoff scale for smoothing for series 1
"""
if cutoff_scale1:
segments = series1.segment()
if isinstance(segments, pyleo.core.multiplegeoseries.MultipleGeoSeries):
smoothed_series_value = []
smoothed_series_time = []
for segment in segments.series_list:
if max(segment.time) - min(segment.time) > 6:
segment_smooth = segment.interp().filter(cutoff_scale=cutoff_scale1)
smoothed_series_value.extend(segment_smooth.value)
smoothed_series_time.extend(segment_smooth.time)
smoothed_series = series1.copy()
smoothed_series.value = smoothed_series_value
smoothed_series.time = smoothed_series_time
else:
smoothed_series = series1.interp().filter(cutoff_scale=cutoff_scale1)
series1 = smoothed_series
smoothed_segments = series1.segment()
series1_values = []
series2_values = []
if isinstance(smoothed_segments, pyleo.core.multiplegeoseries.MultipleGeoSeries):
for segment in smoothed_segments.series_list:
ms = pyleo.MultipleSeries([segment, series2]).common_time()
s1, s2 = ms.series_list
series1_values.extend(s1.value)
series2_values.extend(s2.value)
assert len(series1_values) == len(series2_values)
time = np.arange(len(series1_values))
s1_corr = pyleo.Series(time=time, value=series1_values, verbose=False)
s2_corr = pyleo.Series(time=time, value=series2_values, verbose=False)
else:
s1_corr = series1
s2_corr = series2
corr = s1_corr.correlation(s2_corr, number=1, mute_pbar=True)
return corr
We create some simple, sinusoidal toy data using numpy and a dummy GeoSeries object:
# Creating toy data
toy_time = np.arange(0, 200, 1)
toy_value = np.sin(2 * np.pi * toy_time / 19) + np.sin(2 * np.pi * toy_time / 23)
toy_series = pyleo.GeoSeries(
time=toy_time,
value=toy_value,
time_name="Age",
time_unit="Kyr BP",
label="Toy Series",
value_unit="unitless",
verbose=False,
lat=10,
lon=10,
)
Calculating correlations between toy data and shifted insolation curves#
Here we first create insolation curves for integrated July insolation at latitudes from the equator up to 80N:
# Creating our insolation object
lat_list = np.arange(0, 85, 5)
# array with specified kyears (can be plain numpy or xarray.DataArray)
years = np.arange(-1000, 1)
# subset of orbital parameters for specified time
orb = OrbitalTable.interp(kyear=years)
# Day numbers from June 1st to August 31st
july_days = np.arange(182, 213)
july_dict = {}
for lat in lat_list:
inso = daily_insolation(lat=lat, day=july_days, orb=orb).mean(dim="day")
inso_series = pyleo.Series(
time=0 - years[::-1],
value=inso[::-1],
time_name="Age",
time_unit="Kyr BP",
value_name=f"july Insolation {lat}",
value_unit="W/m^2",
verbose=False,
)
july_dict[lat] = inso_series
Now we calculate the correlation between our toy data and shifted versions of our insolation curves at each latitude:
# Calculating the correlation between shifted versions of our insolation object and our toy data
shift_array = np.arange(
-3.5, 3.6, 1.75
) # Define the leads/lags to be analyzed in units of your time axis (we use kyrs BP here)
# shift_array = np.arange(-8,8.1,2)
series_shift_dict = {shift: {} for shift in shift_array}
shifted_series_dict = {lat: {} for lat in lat_list}
for shift in tqdm(shift_array):
corr_res = {}
for corr_lat, corr_series in july_dict.items():
series = toy_series.copy()
shift_corr_series = corr_series.copy()
shift_corr_series.time += shift
shifted_series_dict[corr_lat][shift] = shift_corr_series
# corr = correlate_hiatus_series(series1=series,series2=shift_corr_series,cutoff_scale1=6)
corr = series.correlation(shift_corr_series, number=1, mute_pbar=True)
corr_res[corr_lat] = [corr.p, corr.r]
correlated_inso = []
for corr_lat, res in corr_res.items():
corr_p, corr_r = res
correlated_inso.append([corr_lat, corr_p, corr_r])
series_shift_dict[shift] = correlated_inso
0%| | 0/5 [00:00<?, ?it/s]
100%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 5/5 [00:00<00:00, 68.55it/s]
The correlation r values are then placed into a pandas DataFrame for easier plotting:
# Putting the results into a dataframe
columns = [math.ceil(a) for a in shift_array * 1000]
shift_df_r = pd.DataFrame(index=np.arange(5, 81, 5), columns=columns)
for shift in shift_array:
corr_list = series_shift_dict[shift]
for corr in corr_list:
lat = np.abs(corr[0])
r = corr[2]
shift_df_r.loc[lat, math.ceil(shift * 1000)] = r
The same is done for r^2 values as well:
# Putting the squared results into a dataframe
columns = [math.ceil(a) for a in shift_array * 1000]
shift_df_r2 = pd.DataFrame(index=np.arange(5, 81, 5), columns=columns)
for shift in shift_array:
corr_list = series_shift_dict[shift]
for corr in corr_list:
lat = np.abs(corr[0])
r = corr[2]
shift_df_r2.loc[lat, math.ceil(shift * 1000)] = r**2
Calculating correlations using different months of insolation instead of different shifts#
Now, instead of calculating correlation between our toy data and shifted insolation, we calculate correlation between toy data and insolation at different months. First we create our insolation dictionary containing insolation at multiple latitudes, integrated over individual summer months:
# Creating our insolation objects
inso_dict = {}
month_dict = {
# 'January' : np.arange(1,32),
# 'February' : np.arange(32,60),
# 'March' : np.arange(60,91),
# 'April' : np.arange(91,121),
"May": np.arange(121, 152),
"June": np.arange(152, 182),
"July": np.arange(182, 213),
"August": np.arange(213, 244),
"September": np.arange(244, 274),
# 'October' : np.arange(274,304),
# 'November' : np.arange(304,335),
# 'December': np.arange(335,365)
} # Key is month number, value is day numbers associated with that month
# array with specified kyears (can be plain numpy or xarray.DataArray)
years = np.arange(-1000, 1)
# subset of orbital parameters for specified time
orb = OrbitalTable.interp(kyear=years)
for month, days in month_dict.items():
inso_dict[month] = {}
for lat in lat_list:
days = month_dict[month]
inso = daily_insolation(lat=lat, day=days, orb=orb).mean(dim="day")
inso_series = pyleo.Series(
time=years,
value=inso,
time_name="Time",
time_unit="Kyr AD",
value_name=f"{month} Insolation {lat}",
value_unit="W/m^2",
verbose=False,
)
inso_dict[month][lat] = inso_series.convert_time_unit("Kyr BP")
Calculating correlation, same as before:
# Calculating the correlation between different months of insolation and our toy data
series_month_dict = {month: {} for month in inso_dict.keys()}
for month in tqdm(series_month_dict.keys()):
series = toy_series.copy()
month_lat_dict = inso_dict[month]
corr_res = {}
for corr_lat, corr_series in month_lat_dict.items():
corr = correlate_hiatus_series(
series1=series, series2=corr_series, cutoff_scale1=6
)
corr_res[corr_lat] = [corr.p, corr.r]
correlated_inso = []
for corr_lat, res in corr_res.items():
corr_p, corr_r = res
correlated_inso.append([corr_lat, corr_p, corr_r])
series_month_dict[month] = correlated_inso
0%| | 0/5 [00:00<?, ?it/s]
80%|███████████████████████████████████████████████████████████████████████████████████████████████████▏ | 4/5 [00:00<00:00, 37.09it/s]
100%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 5/5 [00:00<00:00, 37.19it/s]
Putting the results into DataFrames:
# Putting the results into a dataframe
columns = list(series_month_dict.keys())
month_df_r = pd.DataFrame(index=np.arange(5, 81, 5), columns=columns)
for month in series_month_dict.keys():
corr_list = series_month_dict[month]
for corr in corr_list:
lat = np.abs(corr[0])
r = corr[2]
month_df_r.loc[lat, month] = r
# Putting the squared results into a dataframe
columns = list(series_month_dict.keys())
month_df_r2 = pd.DataFrame(index=np.arange(5, 81, 5), columns=columns)
for month in series_month_dict.keys():
corr_list = series_month_dict[month]
for corr in corr_list:
lat = np.abs(corr[0])
r = corr[2]
month_df_r2.loc[lat, month] = r**2
Creating the multi-panel figure#
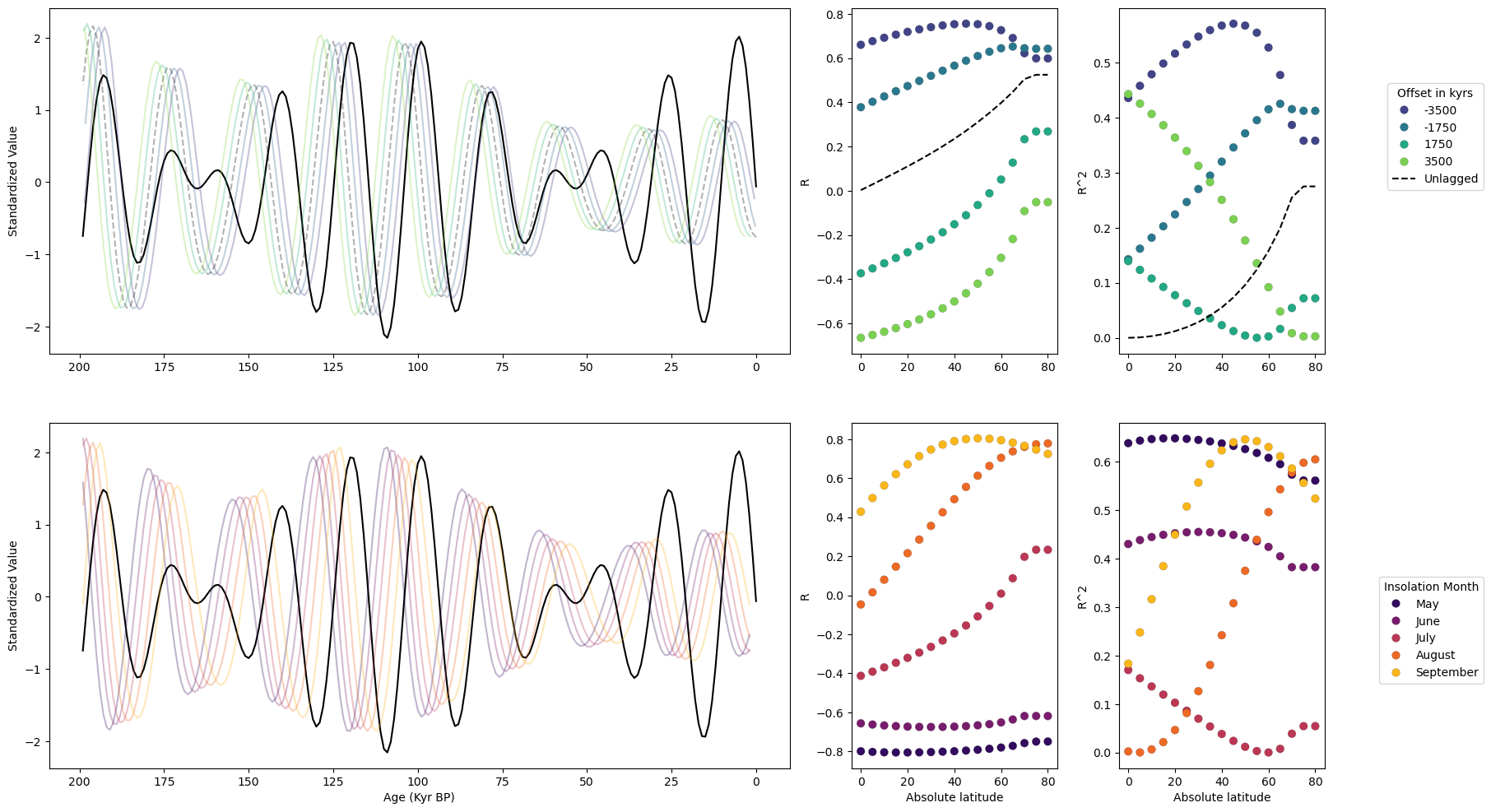
Now, we put everything together and create a multi-panel figure:
# Create a figure
fig = plt.figure(figsize=(20, 12))
# Create a GridSpec object with 2 rows and 2 columns
gs = gridspec.GridSpec(2, 5, wspace=0.3)
# Add subplots using the GridSpec object
ax1 = fig.add_subplot(gs[0, :3])
ax2 = fig.add_subplot(gs[0, 3])
ax3 = fig.add_subplot(gs[0, 4])
ax4 = fig.add_subplot(gs[1, :3])
ax5 = fig.add_subplot(gs[1, 3])
ax6 = fig.add_subplot(gs[1, 4])
# Shift timeseries
shift_colors = sns.color_palette(
"viridis", n_colors=len(shifted_series_dict[10].keys())
)
toy_series.standardize().plot(ax=ax1, color="black", label="Toy Series")
for idx, pair in enumerate(shifted_series_dict[10].items()):
shift, shifted_series = pair
if shift == 0:
shifted_series.slice((min(toy_time), max(toy_time))).standardize().plot(
ax=ax1, label=f"{shift}", alpha=0.3, color="black", linestyle="dashed"
)
else:
shifted_series.slice((min(toy_time), max(toy_time))).standardize().plot(
ax=ax1, label=f"{shift}", alpha=0.3, color=shift_colors[idx]
)
ax1.set_ylabel("Standardized Value")
ax1.set_xlabel("")
ax1.legend().set_visible(False)
ax1.invert_xaxis()
# Shift r plot
shift_df_r_scatter = shift_df_r.drop(labels=0, axis=1)
sns.scatterplot(
shift_df_r_scatter,
ax=ax2,
legend=True,
palette="viridis",
markers=["o" for _ in shift_df_r_scatter.columns],
s=50,
edgecolor="black",
linewidth=0.1,
)
sns.lineplot(
x=shift_df_r[0].index.to_numpy(),
y=shift_df_r[0].to_numpy(),
ax=ax2,
linestyle="--",
color="black",
label="Unlagged",
)
ax2.set_ylabel("R")
# ax2.set_xlabel('Absolute latitude')
ax2.get_legend().remove()
# ax2.set_title(f"R vs. Latitude for {label.split('.')[0]}")
# Shift r^2 plot
shift_df_r2_scatter = shift_df_r2.drop(labels=0, axis=1)
sns.scatterplot(
shift_df_r2_scatter,
ax=ax3,
legend=True,
palette="viridis",
markers=["o" for _ in shift_df_r_scatter.columns],
s=50,
edgecolor="black",
linewidth=0.1,
)
sns.lineplot(
x=shift_df_r2[0].index.to_numpy(),
y=shift_df_r2[0].to_numpy(),
ax=ax3,
linestyle="--",
color="black",
label="Unlagged",
)
handles, labels = ax3.get_legend_handles_labels()
fig.legend(
handles,
labels,
loc="center right",
bbox_to_anchor=[1, 0.75],
title="Offset in kyrs",
)
ax3.set_ylabel("R^2")
# ax3.set_xlabel('Absolute latitude')
ax3.get_legend().remove()
# ax3.set_title(f"R^2 vs. Latitude for {label.split('.')[0]}")
# Month timeseries
month_colors = sns.color_palette("inferno", n_colors=len(month_dict.keys()))
toy_series.standardize().plot(ax=ax4, color="black", label="Toy Series")
for idx, month in enumerate(month_dict.keys()):
inso_dict[month][10].slice((min(toy_time), max(toy_time))).standardize().plot(
ax=ax4, label=f"{month}", alpha=0.3, color=month_colors[idx]
)
ax4.set_ylabel("Standardized Value")
ax4.set_xlabel("Age (Kyr BP)")
ax4.invert_xaxis()
# Month r plot
sns.scatterplot(
month_df_r,
ax=ax5,
legend=True,
palette="inferno",
markers=["o" for _ in month_df_r.columns],
s=50,
edgecolor="black",
linewidth=0.1,
)
ax5.set_ylabel("R")
ax5.set_xlabel("Absolute latitude")
ax5.get_legend().remove()
# ax5.set_title(f"R vs. Latitude for {label.split('.')[0]}")
# Month r^2 plot
sns.scatterplot(
month_df_r2,
ax=ax6,
legend=True,
palette="inferno",
markers=["o" for _ in month_df_r2.columns],
s=50,
edgecolor="black",
linewidth=0.1,
)
handles, labels = ax6.get_legend_handles_labels()
fig.legend(
handles,
labels,
loc="center right",
bbox_to_anchor=[1, 0.25],
title="Insolation Month",
)
ax6.set_ylabel("R^2")
ax6.set_xlabel("Absolute latitude")
ax6.get_legend().remove()
# ax6.set_title(f"R^2 vs. Latitude for {label.split('.')[0]}")