[Fig. 2] Naïve sampling

%load_ext autoreload
%autoreload 2
import pens
import pandas as pd
import matplotlib.pyplot as plt
from num2tex import num2tex
plt.style.use('default')
pens.set_style()

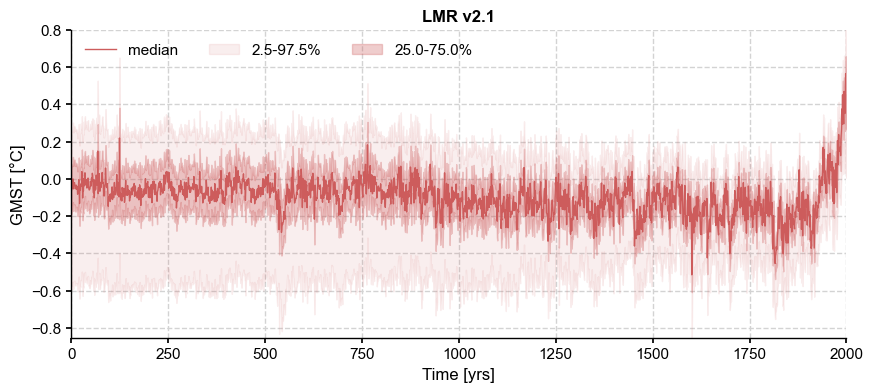
path = '../data/gmt_MCruns_ensemble_full_LMRv2.1.nc'
LMR = pens.EnsembleTS().load_nc(path, var='gmt')
LMR.label = 'LMR v2.1'
LMR.value_name = 'GMST'
LMR.value_unit = '\N{DEGREE SIGN}C'
LMR.time_name = 'Time'
LMR.time_unit = 'yrs'
LMR.plot_qs()

(<Figure size 1000x400 with 1 Axes>,
 <Axes: title={'center': 'LMR v2.1'}, xlabel='Time [yrs]', ylabel='GMST [°C]'>)

df = pd.read_table('../data/PMIP3_GMST.txt')
# create a new pandas.DataFrame to store the processed data
dfn = df.copy()

# remove the data columns for CESM and GISS ensemble members
for i in range(10):
    dfn = dfn.drop([f'CESM_member_{i+1}'], axis=1)

dfn = dfn.drop(['GISS-E2-R_r1i1p127.1'], axis=1)
dfn = dfn.drop(['GISS-E2-R_r1i1p127'], axis=1)
dfn = dfn.drop(['GISS-E2-R_r1i1p121'], axis=1)

# calculate the ensemble mean for CESM and GISS, and add the results into the table
dfn['CESM'] = df[[
    'CESM_member_1',
    'CESM_member_2',
    'CESM_member_3',
    'CESM_member_4',
    'CESM_member_5',
    'CESM_member_6',
    'CESM_member_7',
    'CESM_member_8',
    'CESM_member_9',
    'CESM_member_10',
]].mean(axis=1)

dfn['GISS'] = df[[
    'GISS-E2-R_r1i1p127.1',
    'GISS-E2-R_r1i1p127',
    'GISS-E2-R_r1i1p121',
]].mean(axis=1)

# display the processed data
dfn

	Year	bcc_csm1_1	CCSM4	FGOALS_gl	FGOALS_s2	IPSL_CM5A_LR	MPI_ESM_P	CSIRO	HadCM3	CESM	GISS
0	850	-0.570693	-0.431830	NaN	-0.620995	-0.475963	-0.170230	NaN	-0.620517	0.049553	0.127429
1	851	-0.698903	-0.411177	NaN	-0.753160	-0.742970	-0.303124	-0.398695	-0.553043	0.193858	0.138796
2	852	-0.575440	-0.404802	NaN	-0.743508	-0.758939	-0.422623	-0.406343	-0.560791	0.185033	0.098170
3	853	-0.724757	-0.552719	NaN	-0.869331	-0.746460	-0.335177	-0.353557	-0.438949	0.120470	-0.054552
4	854	-0.724328	-0.734938	NaN	-0.826238	-0.684093	-0.650792	-0.416140	-0.812194	-0.081349	-0.407169
...	...	...	...	...	...	...	...	...	...	...	...
1161	2011	1.013544	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
1162	2012	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
1163	2013	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
1164	2014	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
1165	2015	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN

1166 rows × 11 columns

# store each pyleoclim.Series() object into a dictionary and plot
import pyleoclim as pyleo
ts_dict = {}
for name in dfn.columns[1:]:
    ts_dict[name] = pyleo.Series(
        time=dfn['Year'].values,  # the time axis
        value=dfn[name].values,   # the value axis
        label=name,                  # optional metadata: the nickname of the series
        time_name='Time',            # optional metadata: the name of the time axis
        time_unit='yrs',             # optional metadata: the unit of the time axis
        value_name='GMST',     # optional metadata: the name of the value axis
        value_unit='\N{DEGREE SIGN}C',              # optional metadata: the unit of the value axis
        verbose=False,
    )

ts_list = [v for k, v in ts_dict.items()]  # a pythonic way to convert the pyleo.Series items in the dictionary to a list
ms_pmip = pyleo.MultipleSeries(ts_list)
fig, ax = ms_pmip.plot(lgd_kwargs={
        'bbox_to_anchor': (1.25, 1),  # move the legend to the right side
    })

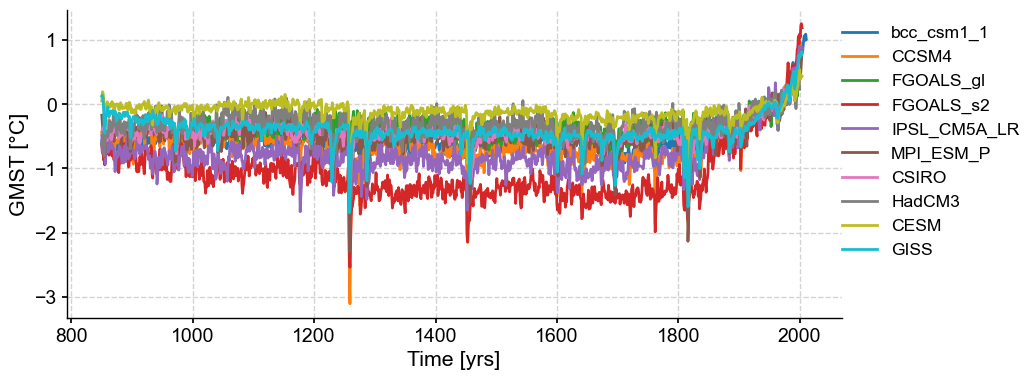
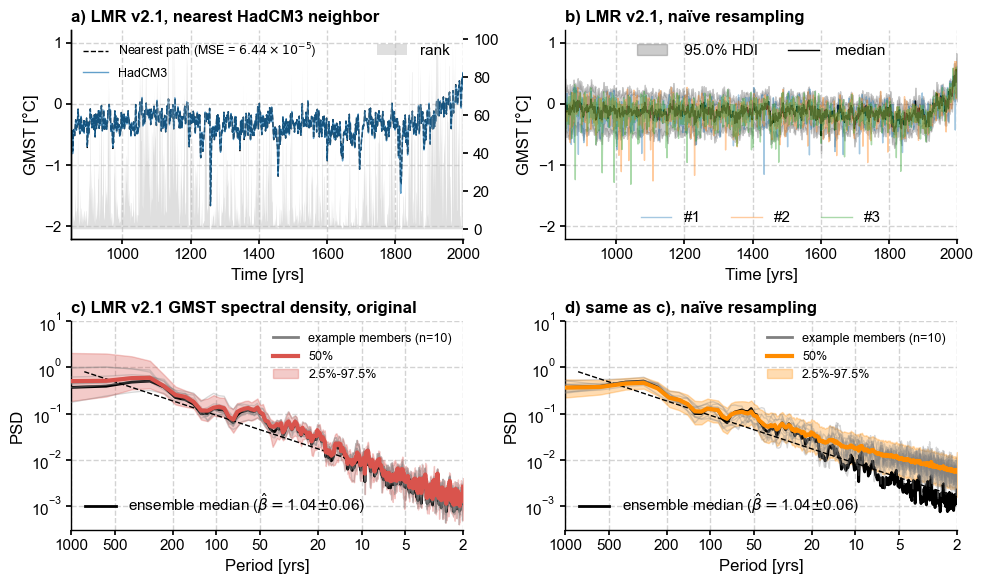
Next we compute the Mean Squared Error between the target series (CCSM4) and all possible trajectories within the ensemble, then find a trajectory that mimimizes it:

ts = ts_list[7] # select HadCM3
common_time = [850,2000]
lmr_slice = LMR.slice(common_time)
HadCM3 = ts.slice(common_time)
path_nearest = lmr_slice.sample_nearest(HadCM3.value, metric='MSE')
dist = path_nearest.distance  # extract distance metric
#
ens_unif = lmr_slice.random_paths(model='unif',p=3, seed=44)
ens_unif.plot(color='tab:green',alpha=0.3)

(<Figure size 1200x400 with 1 Axes>,
 <Axes: xlabel='Time [yrs]', ylabel='GMST [°C]'>)

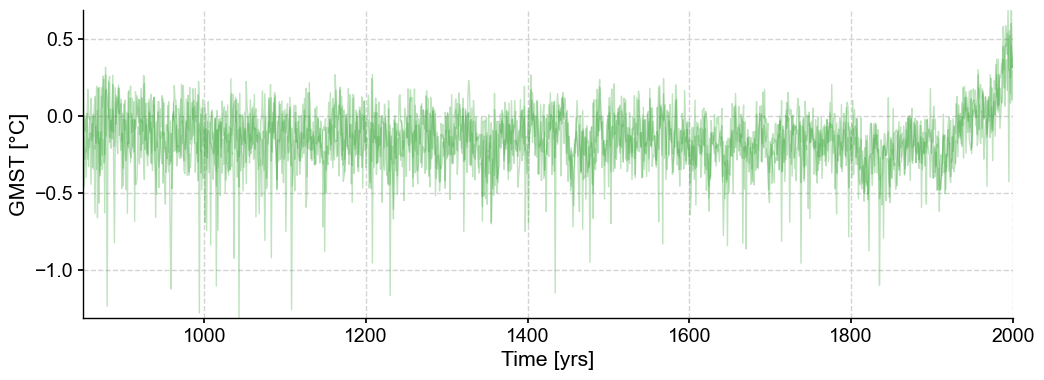
Let’s get the HDI score of each of these.

import numpy as np
ns = ens_unif.nEns
hdi_score = np.zeros((ns))
for k in range(ns):
    hdi_score[k], _ = lmr_slice.hdi_score(y=ens_unif.value[:,k])

Spectral analysis

es_orig = lmr_slice.to_pyleo(verbose=False)
PSD_orig = es_orig.spectral(method='mtm',settings={'standardize':False}) # this generates a MultiplePSD object

Performing spectral analysis on individual series: 100%|██████████| 2000/2000 [00:34<00:00, 57.61it/s]

PSD_orig_aa = PSD_orig.anti_alias()

Applying the anti-alias filter: 100%|██████████| 2000/2000 [00:13<00:00, 148.34it/s]

ps_rnd = lmr_slice.random_paths(model='unif',p=LMR.nEns, seed=2333)
es_rnd = ps_rnd.to_pyleo(verbose=False) # resample while preserving ensemble size
PSD_rnd = es_rnd.spectral(method='mtm',settings={'standardize':False})

Performing spectral analysis on individual series:  93%|█████████▎| 1860/2000 [00:33<00:02, 52.91it/s]

PSD_rnd_aa = PSD_rnd.anti_alias()

Applying the anti-alias filter: 100%|██████████| 2000/2000 [00:17<00:00, 114.54it/s]

percent = lmr_slice.trace_rank(y=HadCM3.value)

Making the figure

fig, axs = plt.subplots(2,2,figsize=(10,6))
axs = axs.flatten()
mse = '{:.2e}'.format(num2tex(dist)) # H/T https://stackoverflow.com/a/54557412
# a) closest match
ax0 = axs[0].twinx()
ax0.grid(False)
ax0.fill_between(lmr_slice.time, 0, percent, alpha=0.5, zorder=0,
                 facecolor='silver', label='rank')
#ax0.set_ylabel('LMR rank (%)')
path_nearest.plot(ax=axs[0],color='k', ls='--', label=rf'Nearest path (MSE = ${mse}$)')
ts.plot(ax=axs[0], ylim=(-2.2, 1.2), alpha=0.7, linewidth=1)
axs[0].legend(loc='upper left', ncol=1, fontsize=9,framealpha = 0.9)
axs[0].set_title('a) LMR v2.1, nearest HadCM3 neighbor',
                 loc = 'left', fontweight = 'bold')
ax0.legend(loc='upper right')
# b) naive resampling
lmr_nolbl = lmr_slice.copy()
lmr_nolbl.label = ''
lmr_nolbl.plot_hdi(prob=0.95, color='k',ax=axs[1],title='')
ens_unif.plot(ax=axs[1],alpha=0.4, label = 'duh', legend_kwargs={'show':True})
axs[1].set_title('b) LMR v2.1, naïve resampling',
                 loc = 'left', fontweight = 'bold')
axs[1].set_ylim(axs[0].get_ylim())
# split the legend in 2 parts
h, l = axs[1].get_legend_handles_labels()
legend1 = axs[1].legend(handles=h[:2], loc='upper center', ncol=2)
axs[1].add_artist(legend1)
l2 = ['#'+str(i+1) for i in range(3)]
legend2 = axs[1].legend(handles=h[2:], labels = l2, loc='lower center', ncol=3)

# c) Undisturbed spectra
ylims = [3e-4,10]
PSD_orig_aa.plot_envelope(ax=axs[2])
axs[2].set_title('c) LMR v2.1 GMST spectral density, original',
                 loc = 'left', fontweight = 'bold')
esm = lmr_slice.get_median() # extract and analyze the ensemble median
esm = esm.to_pyleo(label='ensemble median', verbose=False)
esm_spec = esm.spectral(method ='mtm',settings={'standardize':False})
esm_beta = esm_spec.anti_alias().beta_est() # estimate spectral exponent
esm_beta.plot(ax=axs[2], ylim=ylims, color='k')
h, l = axs[2].get_legend_handles_labels()
legend1 = axs[2].legend(handles=h[:3], loc='upper right',fontsize = 9)
axs[2].add_artist(legend1)
legend2 = axs[2].legend(handles=h[3:], loc='lower left')

# d) Resampled spectra
naive_clr = 'darkorange'
PSD_rnd_aa.plot_envelope(ax=axs[3],curve_clr=naive_clr, shade_clr=naive_clr)
axs[3].set_title('d) same as c), naïve resampling',
                 loc = 'left', fontweight = 'bold')
esm_rnd = ps_rnd.get_median() # extract and analyze the ensemble median
esm_rnd = esm_rnd.to_pyleo(label='ensemble median',verbose=False)
esm_rnd_spec = esm_rnd.spectral(method ='mtm',settings={'standardize':False})
esm_rnd_beta = esm_rnd_spec.anti_alias().beta_est() # estimate spectral exponent
esm_rnd_beta.plot(ax=axs[3],ylim=ylims, color='k', ylabel='PSD')
h, l = axs[3].get_legend_handles_labels()
legend1 = axs[3].legend(handles=h[:3], loc='upper right',fontsize = 9)
axs[3].add_artist(legend1)
legend2 = axs[3].legend(handles=h[3:], loc='lower left')
#axs[3].get_legend().remove()
axs[3].set_xlabel(axs[2].get_xlabel()) # make labels the same
#axs[3].legend(handles=h[3:], loc='lower left')
fig.tight_layout()