Basic timeseries manipulation

by Jordan Landers, Julien Emile-Geay

Preamble

Pyleoclim has multiple functionalities to pre-process a timeseries including standardizing, detrending, and interpolation. You can learn about the various pre-processing steps in Notebooks .ipynb and ipynb. Here, we simply standardize the data and plot it against the original data:

Goals:

• Learn to specify a slice of a Series

• Learn to quickly view summary statistics of a Series

• Learn to standardize a Series

• Learn to gaussianize a Series

Reading Time:

5 minutes

Keywords

Summary Statistics; Standardize; Gaussianize;

Pre-requisites

None. This tutorial assumes basic knowledge of Python. If you are not familiar with this coding language, check out this tutorial.

Relevant Packages

Pandas, Seaborn

Data Description

Sea-surface temperature from Kaplan (1998) averaged over the NINO3 (5N-5S, 150W-190E)) region.

Demonstration

Load a sample dataset

%load_ext watermark

import pyleoclim as pyleo
import pandas as pd
import seaborn as sns

The watermark extension is already loaded. To reload it, use:
  %reload_ext watermark

Pyleoclim ships with a few pre-defined datasets:

pyleo.utils.available_dataset_names()

['SOI', 'NINO3', 'HadCRUT5', 'AIR', 'LR04', 'AACO2', 'EDC-dD', 'GISP2']

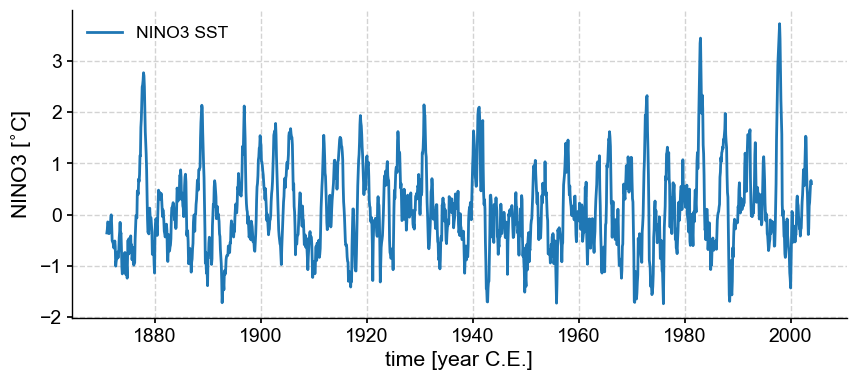
Let’s load the NINO3 timeseries and plot it:

nino3 = pyleo.utils.load_dataset('NINO3')
nino3.plot()

(<Figure size 1000x400 with 1 Axes>,
 <Axes: xlabel='time [year C.E.]', ylabel='NINO3 [$^{\\circ}$C]'>)

Slicing

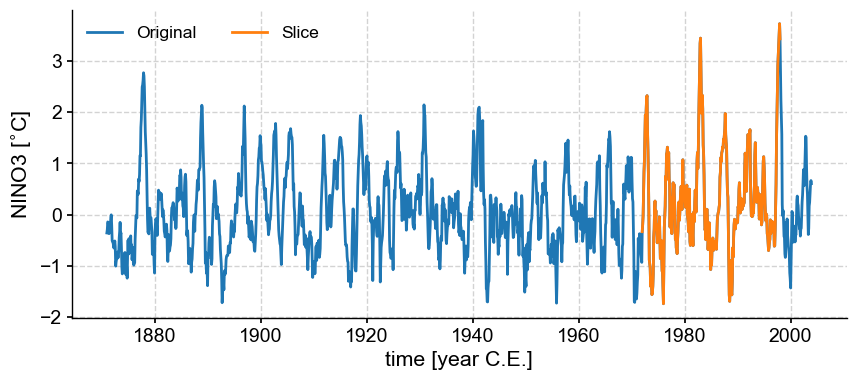
Passing a list containing a pair of dates to .sel() will return the time slice of interest. Notice that the syntax involves “slice”:

nino_slice = nino3.sel(time=slice(1972, 1998))

fig, ax = nino3.plot(label='Original')
nino_slice.plot(label='Slice', color='C1', ax=ax, lgd_kwargs={'ncol': 2})

<Axes: xlabel='time [year C.E.]', ylabel='NINO3 [$^{\\circ}$C]'>

Stats

Calling .stats() will return a handy dictionary of summary statistics (mean, median, min, max, standard deviation, and the interquartile range (IQR))

nino3.stats()

{'mean': 0.07816584993045111,
 'median': -0.022333334,
 'min': -1.739667,
 'max': 3.724903,
 'std': 0.8216852391762094,
 'IQR': 1.015916675}

Or you could do it the pandas way:

nino3.to_pandas().describe()

count    1596.000000
mean        0.078166
std         0.821943
min        -1.739667
25%        -0.487979
50%        -0.022333
75%         0.527937
max         3.724903
Name: NINO3, dtype: float64

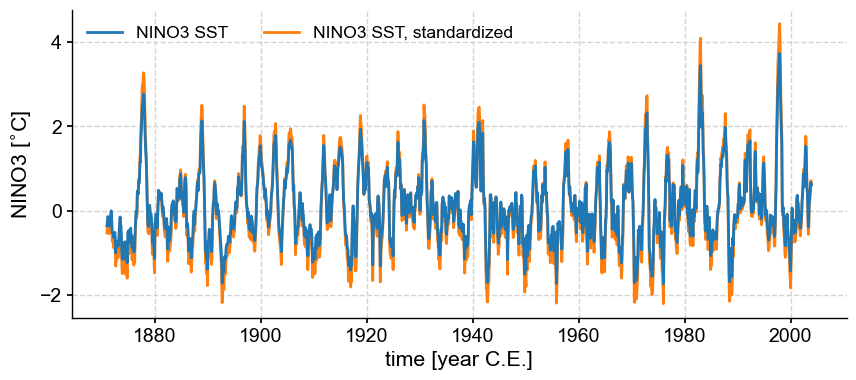
Standardizing

Calling .standardize() subtracts the mean of the series and divides by the standard deviation.

nino3_std = nino3.standardize()
nino3_std.label = nino3.label + ', standardized' 
nino3_std.stats()

{'mean': 1.3356066461656018e-17,
 'median': -0.12230861543917694,
 'min': -2.212322630686346,
 'max': 4.438119338404606,
 'std': 0.9999999999999998,
 'IQR': 1.2363817999438809}

fig, ax = nino3.plot(zorder=99) # this high zorder ensures that it plots on top
ax = nino3_std.plot(ax=ax, lgd_kwargs={'ncol': 2})

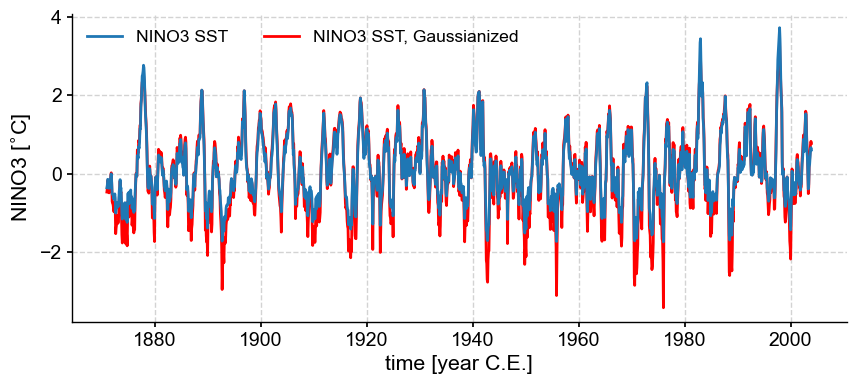
Gaussianize

Calling .gaussianize() maps the series to a standard Gaussian distribution. Not only will it have unit standard deviation (\(\sigma=1\)), a mean (and median) of 0, but its distribution is now the famed Bell Curve. This may be useful for methods that require data to be normally distributed.

nino3_gaus = nino3.gaussianize()
nino3_gaus.label = nino3.label + ', Gaussianized' 
nino3_gaus.stats()

{'mean': 1.3356066461656018e-17,
 'median': 0.0,
 'min': -3.419845799144218,
 'max': 3.419845799144218,
 'std': 0.9995910124024003,
 'IQR': 1.347994295650057}

fig, ax = nino3.plot(zorder=99)
ax = nino3_gaus.plot(ax=ax, lgd_kwargs={'ncol': 2}, **{'color':'red'})

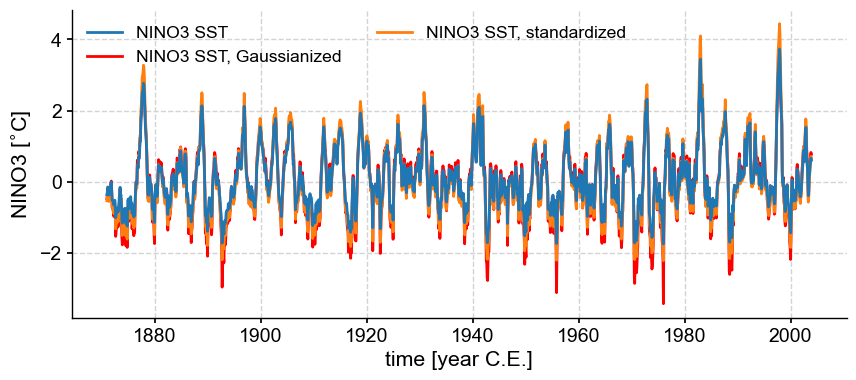
Plotting all of them together:

fig, ax = nino3.plot(zorder=99)
ax = nino3_gaus.plot(ax=ax, lgd_kwargs={'ncol': 2}, **{'color':'red'})
ax = nino3_std.plot(ax=ax, lgd_kwargs={'ncol': 2})

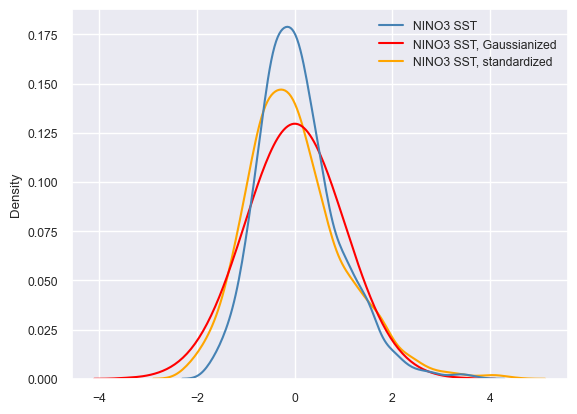
Comparison

For context, it is interesting to compare the different treatments. Seaborn is a very useful plotting library that works very nicely with Pandas. To produce this quick comparison, we will gather those 3 Series into a MultipleSeries object and export it to a Pandas DataFrame. Seaborn will happily ingest this dataframe and return a kernel density plot summarizing the probability density of the data values in each treatment.

nino_ms =  nino3 & nino3_gaus & nino3_std
nino_df = nino_ms.to_pandas()
nino_df

The two series have values differing by more than 1e-05 $^{\circ}$C
Metadata are different:
label property -- left: NINO3 SST, right: NINO3 SST, standardized
The two series have values differing by more than 1e-05 $^{\circ}$C
Metadata are different:
label property -- left: NINO3 SST, Gaussianized, right: NINO3 SST, standardized

	NINO3 SST	NINO3 SST, Gaussianized	NINO3 SST, standardized
datetime
1870-12-31 03:41:38	-0.358250	-0.468084	-0.531123
1871-01-30 14:10:31	-0.292458	-0.377045	-0.451054
1871-03-02 00:39:56	-0.143583	-0.166461	-0.269871
1871-04-01 11:08:49	-0.149625	-0.185602	-0.277224
1871-05-01 21:37:43	-0.274250	-0.348528	-0.428894
...	...	...	...
2003-08-01 04:22:03	0.238497	0.361911	0.195125
2003-08-31 14:51:28	0.411449	0.543054	0.405609
2003-10-01 01:20:21	0.592756	0.752493	0.626262
2003-10-31 11:49:14	0.664131	0.825394	0.713126
2003-11-30 22:18:39	0.604324	0.771389	0.640341

1596 rows × 3 columns

sns.set(font_scale=0.8)
ax = sns.kdeplot(data=nino_df, palette={'NINO3 SST':'steelblue', 'NINO3 SST, Gaussianized':'red', 'NINO3 SST, standardized':'orange'})
ax.legend_.set_title(None)

%watermark -n -u -v -iv -w

Last updated: Mon Mar 04 2024

Python implementation: CPython
Python version       : 3.11.7
IPython version      : 8.20.0

pyleoclim: 0.13.1b0
seaborn  : 0.12.2
pandas   : 2.1.4

Watermark: 2.4.3